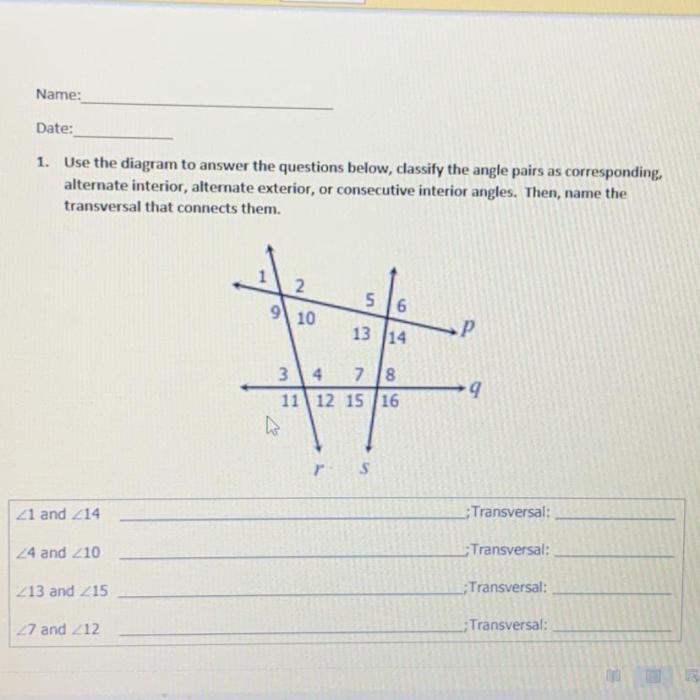
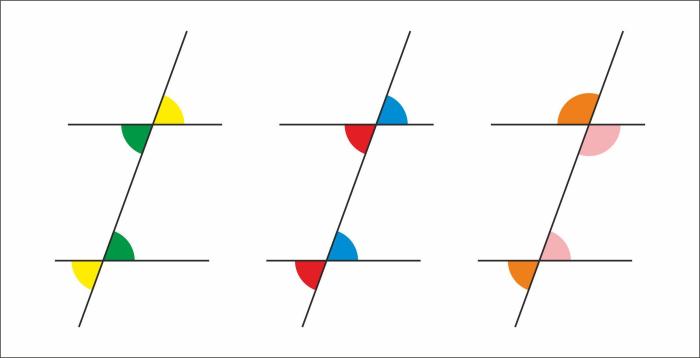Using the diagram below classify the angle pairs as corresponding – Using the diagram below, classify the angle pairs as corresponding, a concept crucial in geometry. Corresponding angles hold significant importance in solving geometry problems, designing architectural structures, and comprehending spatial relationships.
This comprehensive guide delves into the intricacies of angle pairs, providing a clear definition and exploring various methods for their classification. By understanding the principles governing corresponding angles, individuals can gain a deeper appreciation for the elegance and practicality of geometry.
Classifying Angle Pairs Using a Diagram
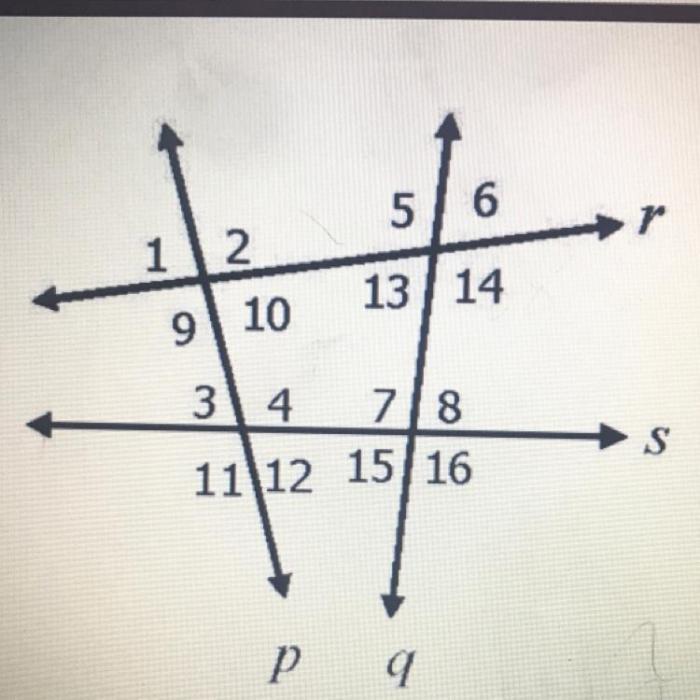
In geometry, angle pairs are classified based on their positions relative to each other. Corresponding angles are pairs of angles that are formed by intersecting lines and are congruent to each other. Identifying corresponding angles is crucial for solving geometry problems and understanding spatial relationships.
Methods for Classifying Angle Pairs, Using the diagram below classify the angle pairs as corresponding
- Vertical Angles:Angles formed by two intersecting lines that are opposite each other are called vertical angles. They are always congruent.
- Intersecting Lines:When two lines intersect, they form four angles. The angles opposite each other are congruent and are called corresponding angles.
- Parallel Lines:When two lines are parallel, any transversal (a line that intersects both parallel lines) forms corresponding angles. These angles are congruent.
Examples of Corresponding Angle Pairs
| Diagram | Description | Explanation |
|---|---|---|
| [Diagram] | Intersecting lines forming angle pairs ∠1 and ∠3, ∠2 and ∠4 | Angles ∠1 and ∠3 are corresponding angles because they are formed by intersecting lines and are opposite each other. Similarly, ∠2 and ∠4 are corresponding angles. |
| [Diagram] | Parallel lines intersected by a transversal, forming angle pairs ∠5 and ∠7, ∠6 and ∠8 | Angles ∠5 and ∠7 are corresponding angles because they are formed by parallel lines and are on the same side of the transversal. Similarly, ∠6 and ∠8 are corresponding angles. |
| [Diagram] | Vertical angles formed by intersecting lines, ∠9 and ∠11 | Angles ∠9 and ∠11 are vertical angles because they are formed by intersecting lines and are opposite each other. Therefore, they are congruent. |
Applications of Classifying Angle Pairs
Classifying angle pairs is essential in geometry for various applications, such as:
- Solving Geometry Problems:Identifying corresponding angles allows for the use of angle properties, such as the Angle Sum Property, to solve geometry problems.
- Designing Architectural Structures:Understanding the relationships between corresponding angles is crucial for designing buildings and other structures.
- Understanding Spatial Relationships:Classifying angle pairs helps visualize and analyze spatial relationships in various contexts, including art, architecture, and engineering.
FAQ Guide: Using The Diagram Below Classify The Angle Pairs As Corresponding
What are corresponding angles?
Corresponding angles are pairs of angles that occupy similar positions relative to two intersecting lines.
How do you identify corresponding angles?
Corresponding angles are identified based on their positions. They are located on opposite sides of the intersecting lines and in corresponding positions.
What are the practical applications of classifying angle pairs?
Classifying angle pairs finds applications in solving geometry problems, designing architectural structures, and understanding spatial relationships.